I've been doing some Javascript recently (well, Coffeescript actually, but this applies equally to either, so I'll stick to Javascript for the examples) and found its approach to objects rather interesting. I think it might be instructive to compare Javascript's objects to Python's, the dynamic programming language I'm most familiar with.
First of all, take this Javascript code, which creates a factory-function called "Counter" which returns objects with "increment" and "decrement" methods:
function Counter() {
this.value = 0
}
Counter.prototype.increment = function() {
this.value += 1;
}
Counter.prototype.decrement = function() {
this.value -= 1;
}
c1 = new Counter()
c2 = new Counter()
c2.increment()
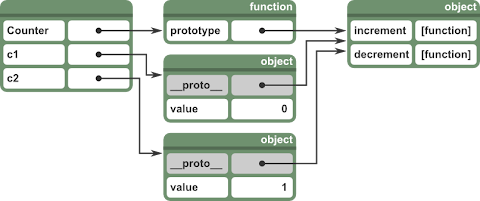
When we execute it, we end with a set of objects much like this:
In our outermost scope (the identity of which I'll gloss over for now) we have three names (or keys) defined. "Counter" is a function object, while "c1" and "c2" are both generic objects. "Counter", like all functions, has an object attached to it under the key "prototype", and it's in this prototype object that we've inserted the functions increment and decrement.
Each time we invoke "new Counter()" a new object is created with its special "__proto__" key mapped to Counter.prototype, and then the Counter function is executed with "this" bound to the new object. The Counter function adds to that object, mapping "value" to the number 0. (I must say, I still don't entirely understand why "new" works like this - I can't see any value in being able to invoke the same function both with and without "new".)
Finally we invoke "c2.increment()". First Javascript looks on the c2 object for the key "increment", but there is no such key. Next, it follows the "__proto__" key and tries again with the prototype object. There it finds the increment function. The function is executed with "this" bound to the "c2" object. When it does "this.value += 1" it first looks up "value" in the same way, finding it directly on the object itself, then after adding 1 to the value it stores it back on the object. (Note that storing something doesn't involve "__proto__" traversal. It always goes straight into the object that you put it into. It's only look-ups that involve "__proto__" traversal.)
Now, let's see the same thing in Python:
class Counter(object):
def __init__(self):
self.value = 0
def increment(self):
self.value += 1
def decrement(self):
self.value -= 1
c1 = Counter()
c2 = Counter()
c2.increment()
At a first glance, things look pretty similar. The "__class__" attributes on the objects are much like the special "__proto__" attributes in Javascript. The "__init__" method is quite similar to the "Counter" function in Javascript. The differences are subtle.
When Python executes the class statement, the three functions "__init__", "increment" and "decrement" are defined and attached to the newly created class object.
When "Counter()" is invoked a bunch of stuff goes on behind the scenes, but importantly a new object instance is created with "__class__" pointing to the class and then the "__init__" function is invoked with the object instance as its first argument.
When "c2.increment()" is executed, first "increment" is looked up on c2. This fails, so next Python follows "__class__" and checks for "increment" on the class. However, something special happens when it finds it there. When an attribute lookup for an object finds a function on its class object, it instead returns a "bound method", which is effectively a function that takes one fewer argument then passes through to the "increment" function itself, inserting a reference to the object as the first argument. So even though the statement "c2.increment()" provides no arguments, when "increment" is actually executed, it receives c2 as its first argument.
There are, I think, two interesting differences here. One is what happens when we want to represent inheritance, which my example doesn't really cover. In Javascript, if attribute lookup fails on the prototype then the prototype's prototype is searched, and so on. In Python, if the attribute lookup fails on the class, then instead of looking at its "__class__" attribute, the base classes are searched. (And since Python allows multiple inheritance, the corner cases are a bit tangled.)
But what I think is most interesting are the different approaches to how methods know their receiving object and the unintuitive consequences of these mechanisms. In Javascript, when a function is retrieved from an object and invoked on the same expression, it triggers the binding of "this" to the object in the function. But if you take a reference to the function and invoke it separately then "this" remains "undefined". For example:
c1.increment();
is not equivalent to this:
var f = c1.increment; f();
The former will increment c1. The latter will do nothing because increment executes with this undefined.
In Python, on the other hand, the equivalent will work as you might expect, because "c1.increment" in fact refers to a bound method. However, from this we can see that in Python "Counter.increment" is not the same entity as "c1.increment". "Counter.increment" is a function that takes one argument. "c1.increment" is a bound method that takes no arguments. In contrast, in Javascript, "Counter.prototype.increment" refers to the exact same object as "c1.increment". So Python does the magic during object attribute lookup, while Javascript does the magic when invoking an attribute as a function.
I think this is all correct, but do let me know if I've made a mistake. I'm finding Javascript a lot more pleasant than I expected, except for its cheerful silent propagation of "undefined" at every opportunity, and Coffeescript definitely rounds off some of the rough corners. In fact, I'd say I even slightly prefer Coffeescript's class notation to Python's.
I'm curious to know if there are any particular benefits of prototype-based objects. I can't see any clear advantages over class-based objects, and I particularly don't understand the benefit of being able to use any function to create an object. Is it just nice because it results in a smaller language? (Does it result in a smaller language?)